计算智能（CI）之粒子群优化算法（PSO）（一）

linjiping

作者：Geppetto

计算智能(Computational Intelligence , CI)是以生物进化的观点认识和模拟智能。按照这一观点，智能是在生物的遗传、变异、生长以及外部环境的自然选择中产生的。在用进废退、优胜劣汰的过程中，适应度高的结构被保存下来，智能水平也随之提高。因此计算智能就是基于结构演化的智能。计算智能的主要方法有人工神经网络、遗传算法、遗传程序、演化程序、局部搜索、模拟退火等等。这些方法具有以下共同的要素：自适应的结构、随机产生的或指定的初始状态、适应度的评测函数、修改结构的操作、系统状态存储器、终止计算的条件、指示结果的方法、控制过程的参数。计算智能的这些方法具有自学习、自组织、自适应的特征和简单、通用、鲁棒性强、适于并行处理的优点。在并行搜索、联想记忆、模式识别、知识自动获取等方面得到了广泛的应用。典型的代表如遗传算法、免疫算法、模拟退火算法、蚁群算法、微粒群算法，都是一种仿生算法，基于“从大自然中获取智慧”的理念，通过人们对自然界独特规律的认知，提取出适合获取知识的一套计算工具。总的来说，通过自适应学习的特性，这些算法达到了全局优化的目的。

粒子群优化算法(Partiele Swarm Optimization , PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。由Kennedy和Eberhart博士于1995年提出，是一种基于群智能(Swarm Intelligence , SI)方法的演化计算(Evolutionary Computation , EC)技术，可通过微利之间的相互作用发现复杂搜索空间中的最优区域。

鸟被抽象为没有质量和体积的微粒(点)，并延伸到N维空间，粒子I在N维空间的位置表示为矢量Xi＝(x1,x2,…,xN)，飞行速度表示为矢量Vi＝(v1,v2,…,vN)．每个粒子都有一个由目标函数决定的适应值(fitness value)，并且知道自己到目前为止发现的最好位置(pbest)和现在的位置Xi．这个可以看作是粒子自己的飞行经验．除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是pbest中的最好值)．这个可以看作是粒子同伴的经验．粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。

Millonas在开发人工生命算法时(1994年)，提出群体智能概念并提出五点原则：

1.接近性原则：群体应能够实现简单的时空计算；

2.优质性原则：群体能够响应环境要素；

3.变化相应原则：群体不应把自己的活动限制在一狭小范围；

4.稳定性原则：群体不应每次随环境改变自己的模式；

5.适应性原则：群体的模式应在计算代价值得的时候改变。

下面介绍最原始的PSO算法，它公式的内涵也就是基于这5点原则的。

初始化粒子位置：按一定策略，随机生成一些粒子初试位置(随机解)。

通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置

位置更新公式：

速度更新公式：

更新公式中，i=1,2…,N，N是此群中粒子的总数。rand()用于产生（0,1）之间的随机数。C1和C2是学习因子，通常设置为C1=C2=2。

改进后的离散二进制PSO（Binary PSO , BPSO）：

PSO主要优化连续实值问题，BPSO主要优化离散空间约束问题；

BPSO是在离散粒子群算法基础上，约定位置向量、速度向量均由0、1值构成。

初始化粒子位置：按一定策略，生成二进制编码。

速度更新公式：

但没有原始PSO的粒子位置更新公式，为了表示速度的值是二进制位取1的概率，速度的值被映射到区间[0,1]，映射的方法一般采用（2）式sigmoid函数：

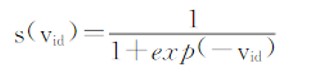
这里s(vid)表示位置xid取1的概率，粒子通过（3）式更新位置：

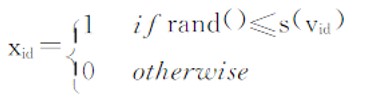
BPSO有很强全局搜索能力，但不能收敛于全局最优值，且随着算法迭代搜索随机性越来越强，缺乏后期的局部搜索能力。

实验：使用BPSO，借助MATLAB优化函数3cos(x(1)x(2)) + x(1) + x(2)^2

参数设置为：

群体粒子个数N=100，粒子维度D=2，最大迭代次数T=200；C1=C2=1.5，惯性权重W∈[0.4,0.8]，位置值x∈[-4,4]，速度值v∈[-1,1]。

实验代码如下：

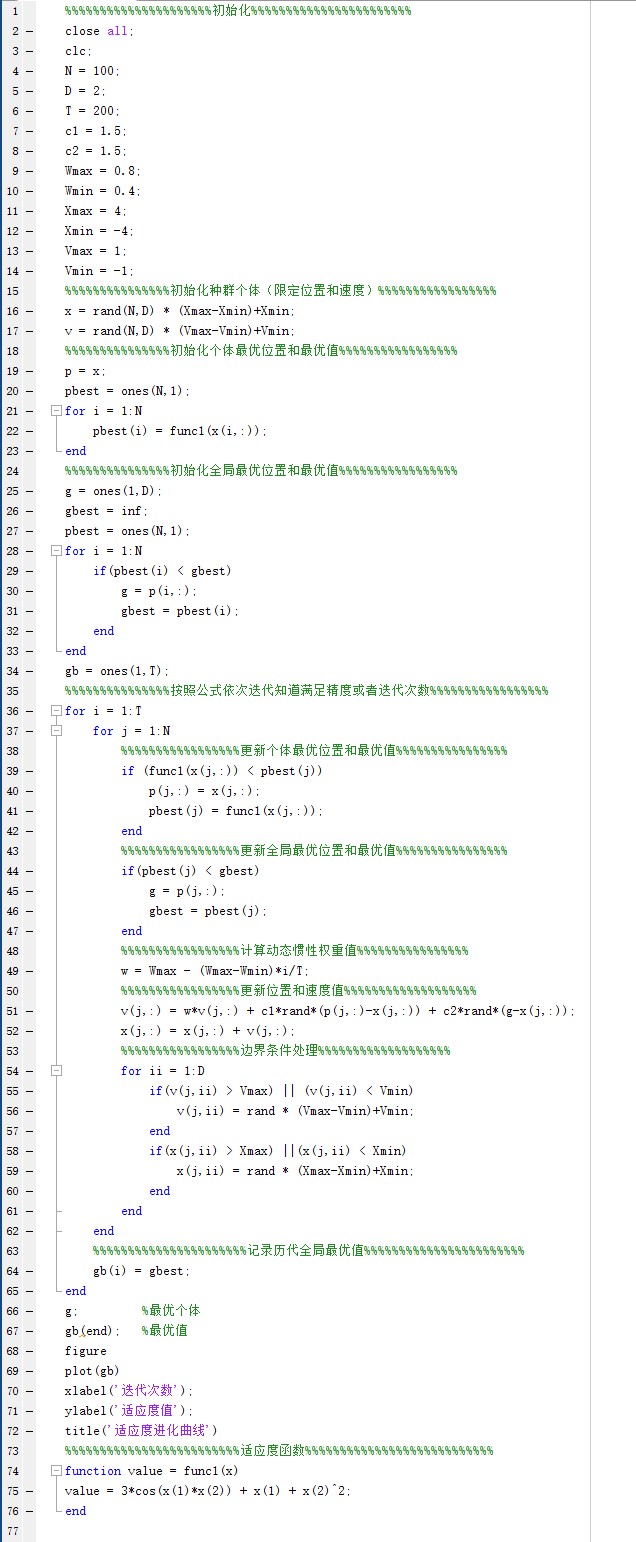
实验结果如下：

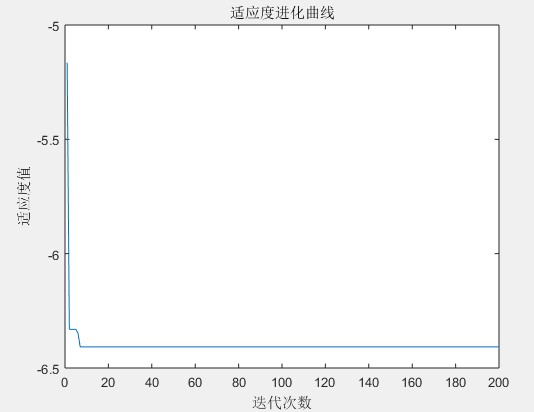
从实验结果可以看出，在迭代大约十次之后，适应度值趋于平稳，说明此值是最优解。

PSO算法的应用：

由于PSO算法概念简单、调参少、容易实现等特点，现已成功的应用于诸多领域。目前主要的应用领域包括以下几个方面：

  1. 优化问题的求解。PSO算法可用于约束优化问题、多目标优化问题、离散空间组合优化问题以及动态跟踪优化问题的求解。
  2. 模式识别和图像处理。PSO算法已在图像分割、图像配准、图像融合、图像识别、图像压缩和图像合成等方面得到成功应用。
  3. 神经网络训练。PSO算法可完成人工神经网络中的各种任务，包括连接权值的训练、结构设计、学习规则调整、特征选择、连接权值的初始化和规则提取等。
  4. 电力系统设计。日本的Fuji电力公司的研究人员将电力企业某个著名的RPVC(Reactive Power and Voltage Control)问题简化为函数的最小值问题，并使用改进的PSO算法进行优化求解。与传统方法如专家系统、敏感性分析相比，实验产生的结果证明了PSO算法在解决该问题的优势。
  5. 半导体器件综合。半导体器件综合是在给定的搜索空间内根据期望得到的器件特性来得到相应的设计参数，一般情况下使用器件模拟器通常得到的特性空间是高度非线性的，因此很难用传统方法来计算，利用PSO算法能比遗传算法更快更好地找到较高质量的设计参数。
  6. 其他应用。除了以上领域外，PSO在自动目标检测、生物信号识别、决策调度、系统识别以及游戏训练等方面也取得了一定的研究成果。

 

 

参考文献

《计算智能基础》 主编：张汝波、刘冠群、吴俊伟

《智能优化算法及其MATLAB实例》 主编：包子阳、余继周

 

Related posts